二连杆机械臂动力学推导（不考虑重力）

前言

前一阵子上了多体动力学的课，动力学方法里主流的两个流派有牛顿欧拉法和拉格朗日法，跟着老师上课也自己看书，梳理讲了一个二连杆机械臂的动力学推导，但是没有给具体的证明，自己按拉格朗日法写一下加深一下理解吧。

二连杆机械臂的动力学推导

书上给出了不考虑重力的动力学公式为：

Image

这里的$p_1$、$p_2$、$p_3$、$q_1$、$q_2$都是什么东西？写得不清不楚的，不过推导动力学用拉格朗日是传统艺能了，我们就来推导一下。

不考虑重力、摩擦力和干扰，那我们就不用考虑系统的势能了。

Image

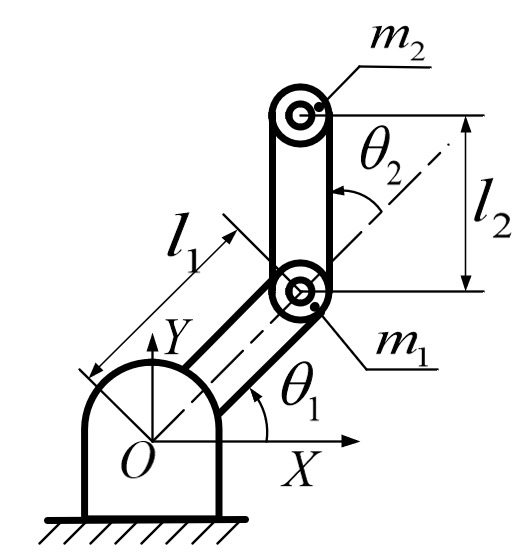
作为一个二关节机械臂，我们认为连杆的质量都集中在末端,旋转关节都在始端，两个旋转关节的旋转角度分别如图旋转$\theta_1$和$\theta_2$，我们取它们作为广义坐标。

从基座如图建立平面坐标系，我们可以写出每个连杆末端旋转副的位置.第一个连杆$X$方向和$Y$方向的坐标为：

$$\begin{aligned} &x_1=l_1\cos\theta_1\\ &y_1=l_1\sin\theta_1 \end{aligned}$$

第二个连杆$X$方向和$Y$方向的坐标为：

$$\begin{aligned} &x_2=l_1\cos\theta_1+l_2\cos(\theta_1+\theta_2)\\ &y_2=l_1\sin\theta_1+l_2\sin(\theta_1+\theta_2) \end{aligned}$$

第一个连杆$X$方向和$Y$方向的速度（对时间求导）为：

$$\begin{aligned} &\dot{x}_1=-l_1\sin\theta_1\,\dot{\theta_1}\\ &\dot{y}_1=l_1\cos\theta_1\,\dot{\theta_1} \end{aligned}$$

第二个连杆$X$方向和$Y$方向的速度（对时间求导）为：

$$\begin{aligned} &\dot{x}_2=-l_1\sin\theta_1\,\dot{\theta_1}-l_2\sin(\theta_1+\theta_2)(\dot{\theta_1}+\dot{\theta_2})\\ &\dot{y}_2=l_1\cos\theta_1\,\dot{\theta_1}+l_2\cos(\theta_1+\theta_2)(\dot{\theta_1}+\dot{\theta_2}) \end{aligned}$$

第一个连杆的动能：

$$\begin{aligned} T_1&=\frac{1}{2}m_1(\dot{x}_1^2+\dot{y}_1^2)\\ &=\frac{1}{2}m_1\left[\left(-l_1\sin\theta_1\,\dot{\theta_1}\right)^2+\left(l_1\cos\theta_1\,\dot{\theta_1}\right)^2\right]\\ &=\frac{1}{2}m_1l_1^2\dot{\theta}_1^2 \end{aligned}$$

第二个连杆的动能：

$$\begin{aligned} T_2&=\frac{1}{2}m_2(\dot{x}_2^2+\dot{y}_2^2)\\ &=\frac{1}{2}m_2\Biggr\{\left[-l_1\sin\theta_1\,\dot{\theta_1}-l_2\sin(\theta_1+\theta_2)(\dot{\theta_1}+\dot{\theta_2})\right]^2\\&\quad +\left[l_1\cos\theta_1\,\dot{\theta_1}+l_2\cos(\theta_1+\theta_2)(\dot{\theta_1}+\dot{\theta_2}))\right]^2\Biggr\}\\ &=\frac{1}{2}m_2\left[l_1^2\dot{\theta}_1^2+l_2^2(\dot{\theta}_1+\dot{\theta}_2)^2+2l_1l_2\dot{\theta}_1(\dot{\theta}_1+\dot{\theta}_2)\cos\theta_2\right] \end{aligned}$$

由于不考虑重力、摩擦力和干扰，于是系统的总能量就是两个动能之和，记作$L$。

$$\begin{aligned} L&=T_1+T_2\\ &=\frac{1}{2}m_1l_1^2\dot{\theta}_1^2+\frac{1}{2}m_2\left[l_1^2\dot{\theta}_1^2+l_2^2(\dot{\theta}_1+\dot{\theta}_2)^2+2l_1l_2\dot{\theta}_1(\dot{\theta}_1+\dot{\theta}_2)\cos\theta_2\right]\\ &=\frac{1}{2}m_1l_1^2\dot{\theta}_1^2+\frac{1}{2}m_2l_1^2\dot{\theta}_1^2+\frac{1}{2}m_2l_2^2\dot{\theta}_1^2+m_2l_2^2\dot{\theta}_1\dot{\theta}_2+\frac{1}{2}m_2l_2^2\dot{\theta}_2^2+m_2l_1l_2(\dot{\theta}_1^2+\dot{\theta}_1\dot{\theta}_2)\cos\theta_2 \end{aligned}$$

机器人在连杆1和连杆2的驱动关节力矩分别是$\tau_1$和$\tau_2$，利用拉格朗日公式有：

$$\begin{aligned} &\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta_1}}\right)-\frac{\partial L}{\partial \theta_1}=\tau_1\\ &\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta_2}}\right)-\frac{\partial L}{\partial \theta_2}=\tau_2 \end{aligned}$$

代入上面的公式有：

$$\begin{aligned} \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta_1}}\right)=&m_1l_1^2\ddot{\theta_1}+m_2l_1^2\ddot{\theta}_1+m_2l_2^2\ddot{\theta}_1+m_2l_2^2\ddot{\theta}_2\\&+2m_2l_1l_2\cos\theta_2\,\ddot{\theta}_1-2m_2l_1l_2\sin\theta_2\,\dot{\theta}_1\dot{\theta}_2\\&+m_2l_1l_2\cos\theta_2\,\ddot{\theta}_2-m_2l_1l_2\sin\theta_2\,\dot{\theta}_2^2\\ \end{aligned}$$

$$\begin{aligned} \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta_2}}\right)=&m_2l_2^2\ddot{\theta}_1+m_2l_2^2\ddot{\theta}_2+m_2l_1l_2\cos\theta_2\,\ddot{\theta}_1\\&-m_2l_1l_2\sin\theta_2\,\dot{\theta}_1\dot{\theta}_2\\ \end{aligned}$$

$$\begin{aligned} \frac{\partial L}{\partial \theta_1}=0 \end{aligned}$$

$$\begin{aligned} \frac{\partial L}{\partial \theta_2}=m_2l_1l_2\dot{\theta}_1^2\sin\theta_2+m_2l_1l_2\dot{\theta}_1\dot{\theta}_2\sin\theta_2 \end{aligned}$$

整理以后我们就有：

$$\begin{aligned} &(m_1l_1^2+m_2l_1^2+m_2l_2^2+2m_2l_1l_2\cos\theta_2)\ddot{\theta}_1+(m_2l_1l_2\cos\theta_2+m_2l_2^2)\ddot{\theta}_2\\&-2m_2l_1l_2\sin\theta_2\dot{\theta}_1\dot{\theta}_2-m_2l_1l_2\sin\theta_2\dot{\theta}_2^2=\tau_1 \end{aligned}$$

$$\begin{aligned} &(m_2l_1l_2\cos\theta_2+m_2l_2^2)\ddot{\theta}_1+m_2l_2^2\ddot{\theta}_2+m_2l_1l_2\sin\theta_2\dot{\theta}_1^2=\tau_2 \end{aligned}$$

于是我们就可以写成书中的形式，描述为矩阵非常简洁的形式：

$$\begin{aligned} \mathbf{D(q)\ddot{q}+C(q,\dot{q})\dot{q}}=\bm{\tau} \end{aligned}$$

其中：

$$\mathbf{D(q)}=\begin{bmatrix} m_1l_1^2+m_2l_1^2+m_2l_2^2+2m_2l_1l_2\cos\theta_2 & m_2l_1l_2\cos\theta_2+m_2l_2^2\\ m_2l_1l_2\cos\theta_2+m_2l_2^2 & m_2l_2^2 \end{bmatrix}$$

$$\mathbf{C(q,\dot{q})}=\begin{bmatrix} -m_2l_1l_2\sin\theta_2\dot{\theta}_2 & -m_2l_1l_2\sin\theta_2\dot{\theta}_1-m_2l_1l_2\sin\theta_2\dot{\theta}_2\\ m_2l_1l_2\sin\theta_2\dot{\theta}_1 & 0 \end{bmatrix}$$

$$\mathbf{q}=\begin{bmatrix} \theta_1\\ \theta_2 \end{bmatrix}\quad \dot{\mathbf{q}}=\begin{bmatrix} \dot{\theta}_1\\ \dot{\theta}_2 \end{bmatrix}\quad \bm{\tau}=\begin{bmatrix} {\tau}_1\\ {\tau}_2 \end{bmatrix}$$

这也就解释了开头书中的公式：

Image

其中

$$\begin{aligned} p_1&=m_1l_1^2+m_2l_1^2\\ p_2&=m_2l_2^2\\ p_2&=m_2l_1l_2 \end{aligned}$$