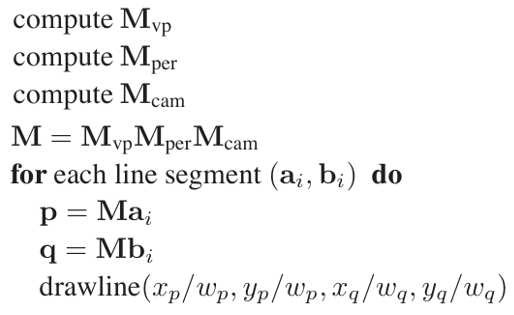计算机图形学基础

1 Transformation Matrix-变换矩阵

另外要注意的是：

1. 运动的合成根据的是矩阵左乘规则，因为参考坐标系始终是固定坐标系。

2. 下面的齐次坐标是等价的：

$$(x, y, z, 1)\triangleq(k x, k y, k z, k !=0)$$

例子：$(1,0,0,1)$ 和$(2,0,0,2)$ 都表示$(1,0,0)$

2 Viewing-观测

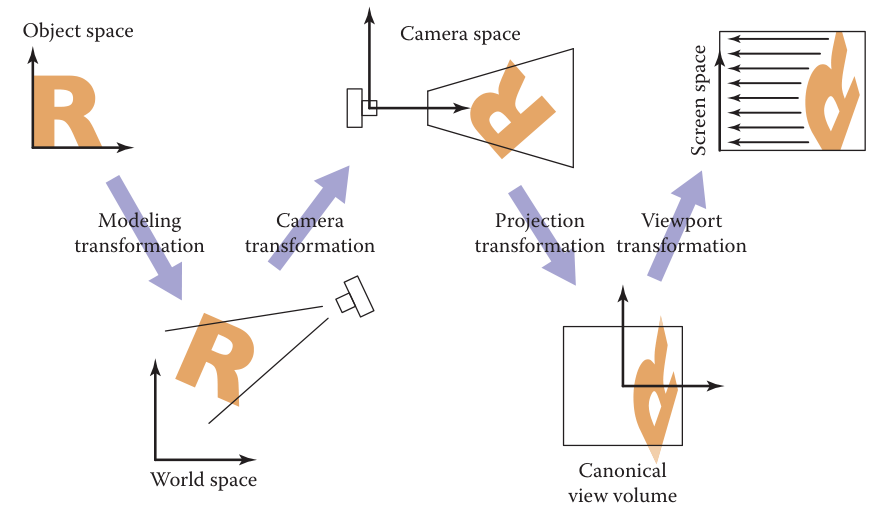
观测主要解决的问题是如何把物体的三维“模型”变成我们在屏幕所看到的二维“图片”，我们在计算机看到实体模型可以分成这样几步：

物体空间如何经过一系列变换转化到屏幕上

• 相机变换(camera transformation)或眼变换(eye transformation)：想象把相机放在任意一个位置来观测物体，我们首先就要把物体的世界坐标转换为相机坐标，这一步称为相机变换或眼变换。
• 投影变换(projection transformation)：相机把物体拍成照片本质是从三维的相机坐标转化为二维的平面坐标，这一步称为投影变换。投影可以分为正射投影和透视投影。
• 视口变换(viewport transformation)或窗口变换(windowing transformation)：相机拍成的图片最后是要显示在屏幕上，我们需要把二维的图片坐标再转换为电脑屏幕的像素坐标，这一步称为视口变换或窗口变换。

下面这个照相的类比非常地生动形象。

观测的形象解释

2.1 Viewport Transformation-视口变换

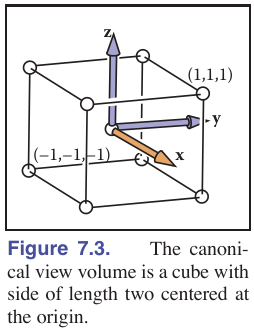
一般来说，我们规定相机沿着$-\mathbf{z}$方向，在观测过程中为了简化会使用canonical view volume(CCV)：它是一个正方体，$x$,$y$,$z$坐标都位于$-1$到$1$之间，也即$(x,y,z)\in[-1,1]^3$，我们将$x=-1$投影到电脑屏幕的左侧，将$x=+1$投影到屏幕的右侧，将$y=-1$投影到屏幕的底部，将$y=+1$投影到屏幕的顶部。

canonical view volume(CCV)

如果我们定义屏幕每个像素的长和宽为1，最小的像素中心坐标是$(0,0)$，则图像的中心到其边界为$0.5$，如果屏幕上的像素总长度为$n_x$，总宽度为$n_y$，那么我们可以将canonical view volume(CCV)的$\mathbf{xoy}$平面的方形$[-1,1]^2$映射为长方形$[-0.5,n_x-0.5]\times[-0.5,n_y-0.5]$。

注意我们现在假设所有的线都在CCV正方体里，后面这个假设将在讲裁剪的时候放松这个条件。

对于视口变换，我们需要想把CCV正方体的$\mathbf{xoy}$平面进行放缩然后将原点平移到屏幕的左下角（CCV的原点在$\mathbf{xoy}$正方形的正中心），其可以写作一个二维的变换【这里相当于计算上面的线性映射：$-1\rightarrow -0.5,1\rightarrow n_x-0.5($或$n_y-0.5)$】：

$$\begin{bmatrix} x_{\text {screen }} \\ y_{\text {screen }} \\ 1 \end{bmatrix}=\begin{bmatrix} \frac{n_{x}}{2} & 0 & \frac{n_{x}-1}{2} \\ 0 & \frac{n_{y}}{2} & \frac{n_{y}-1}{2} \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x_{\text {canonical }} \\ y_{\text {canonical }} \\ 1 \end{bmatrix}$$

这里忽略了$\mathbf{z}$轴的坐标，因为投影最终和$z$坐标无关，这里我们可以扩充矩阵（尽管在这里没有用）：

$$\mathbf{M}_{\mathrm{vp}}=\begin{bmatrix} \frac{n_{x}}{2} & 0 & 0 & \frac{n_{x}-1}{2} \\ 0 & \frac{n_{y}}{2} & 0 & \frac{n_{y}-1}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$

2.2 Orthographic Projection Transformation-正射变换

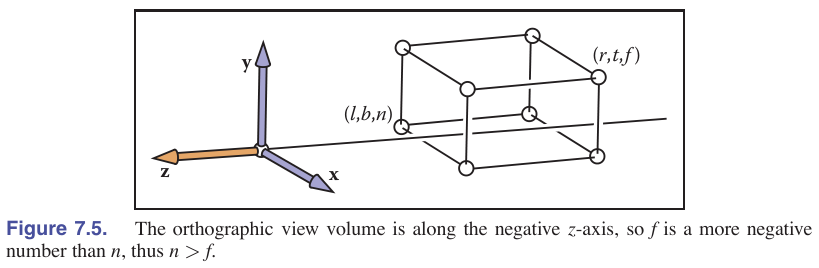
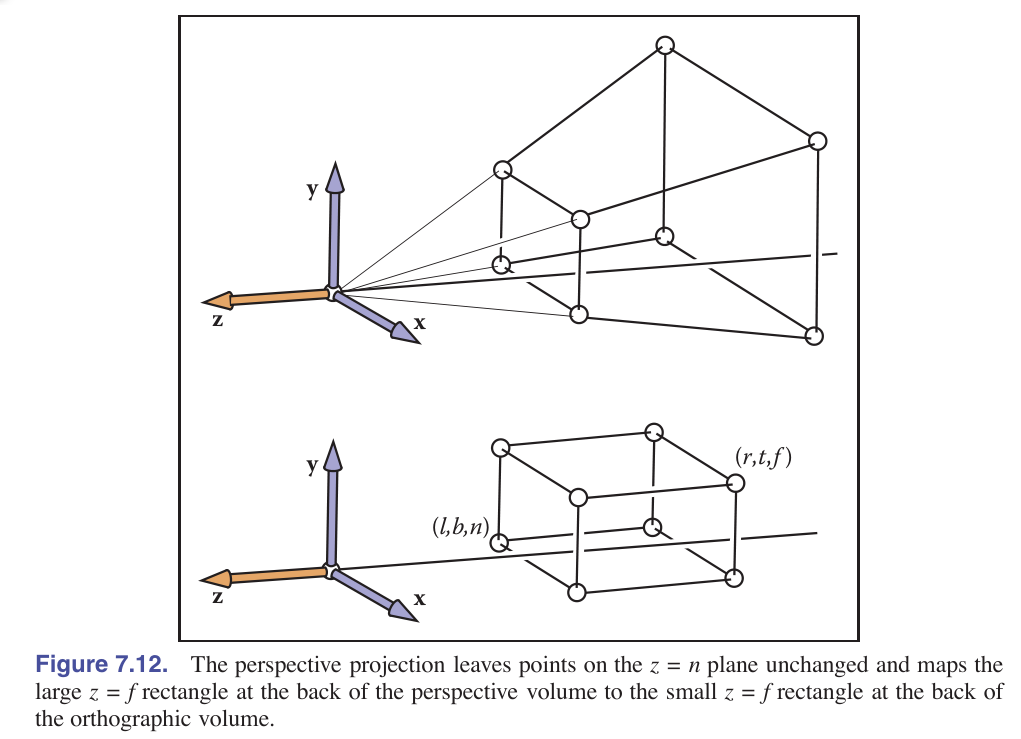
我们通常想把在渲染某个空间区域的几何元素而不是CCV，我们要调整我们的坐标轴的方向来实现正射变换，让坐标轴的$-\mathbf{z}$轴对着物体，让$\mathbf{y}$轴朝上，$\mathbf{x}$轴按照右手定则定义。我们看到的view volume是一个$[l,r]\times[b,t]\times[f,n]$的box。

正射变换

关于$l,r,b,y,f,n$的物理含义可以看下面的表格：

我们同样可以写出变换矩阵把这个box映射为CCV（参考原书公式的6.7，英文原版132页）,变换的好处是简化数字在$-1$到$1$之间，方便后续计算：

$$\begin{aligned}\mathbf{M}_{\text {orth }}&=\left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{array}\right]\\&=\begin{bmatrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f} \\ 0 & 0 & 0 & 1 \end{bmatrix}\end{aligned}$$

现在我们可以转换视角中任意看到的点$(x,y,z)$在像素上看到的位置$(x_{pixel},y_{pixel},z_{canonical})$

$$\left[\begin{array}{c} x_{\text {pixel }} \\ y_{\text {pixel }} \\ z_{\text {canonical }} \\ 1 \end{array}\right]=\left(\mathbf{M}_{\mathrm{vp}} \mathbf{M}_{\text {orth }}\right)\left[\begin{array}{c} x \\ y \\ z \\ 1 \end{array}\right]$$

CCV坐标变换至屏幕坐标直线算法流程：

CCV变换至屏幕坐标直线

$\mathbf{z}$坐标的范围是$[-1,1]$，现在我们还没有用到，这将在z-buffer算法时很有用。

2.3 Camera Transformation-相机变换

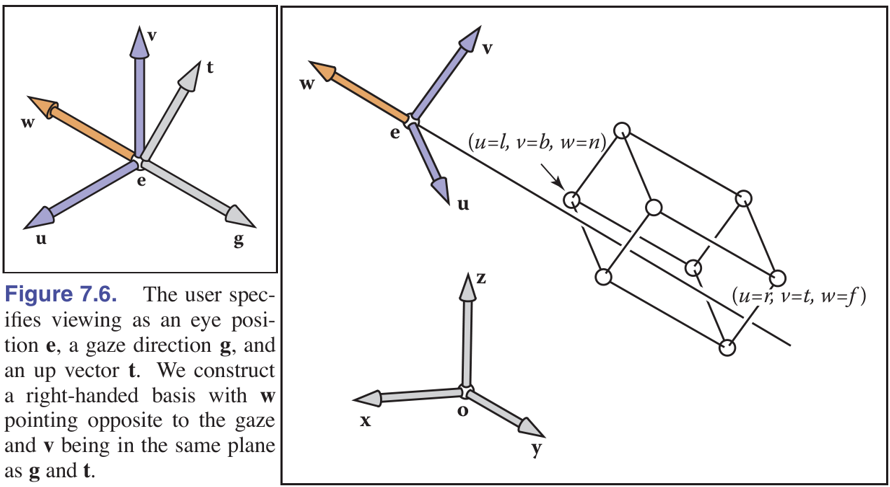
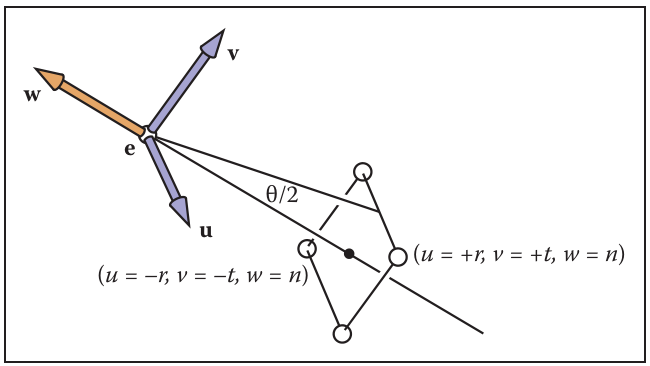
当我们需要改变3D视角和观测的方向时，我们需要重新定义观测者的位置和方向（改变相机的放置位置）。可以定义相机坐标系，我们期望的相机的朝向可以由两个向量$\mathbf{g}$和向量$\mathbf{t}$来定义，以及一个点$\mathbf{e}$来表示。

• $\mathbf{e}$：相机位置
• $\mathbf{g}$：观测方向
• $\mathbf{t}$：上视方向

于是我们可以根据上面所说的向量和电定义我们的相机坐标系$\mathbf{uvw}$（世界坐标系是$\mathbf{xyz}$），其中坐标系的原点就是$\mathbf{e}$，$\mathbf{v}$轴和$\mathbf{t}$矢量方向相同，$\mathbf{w}$轴和$-\mathbf{g}$矢量方向相同，$\mathbf{u}$轴根据右手定则确定。

$$\begin{aligned} \mathbf{w} & = -\frac{\mathbf{g}}{\|\mathbf{g}\|} \\ \mathbf{u} & = \frac{\mathbf{t} \times \mathbf{w}}{\|\mathbf{t} \times \mathbf{w}\|} \\ \mathbf{v} & = \mathbf{w} \times \mathbf{u} \end{aligned}$$

相机坐标系

接下来我们会把世界坐标系的点坐标转换到相机坐标系中。我们可以把变换矩阵分解为两步，先平移再旋转。

由于将坐标系$\mathbf{uvw}$转换为坐标系$\mathbf{xyz}$的变换矩阵可以看做是

$$\mathbf{M}_{\mathrm{cam}}^{-1}=\left[\begin{array}{cccc} \mathbf{u} & \mathbf{v} & \mathbf{w} & \mathbf{e} \\ 0 & 0 & 0 & 1 \end{array}\right]$$

相机坐标系是要将坐标系$\mathbf{xyz}$转换到坐标系$\mathbf{uvw}$，于是这等价于对矩阵求一个逆。

$$\mathbf{M}_{\mathrm{cam}}=\left[\begin{array}{cccc} \mathbf{u} & \mathbf{v} & \mathbf{w} & \mathbf{e} \\ 0 & 0 & 0 & 1 \end{array}\right]^{-1}=\left[\begin{array}{cccc} x_{u} & y_{u} & z_{u} & 0 \\ x_{v} & y_{v} & z_{v} & 0 \\ x_{w} & y_{w} & z_{w} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} 1 & 0 & 0 & -x_{e} \\ 0 & 1 & 0 & -y_{e} \\ 0 & 0 & 1 & -z_{e} \\ 0 & 0 & 0 & 1 \end{array}\right]$$

世界坐标正式投影变换至屏幕坐标画直线算法流程：

世界坐标正式投影变换至屏幕坐标画直线

2.4 Perspective Projective Transformations-透视变换

投影变换符合我们的视觉直观，主要体现在有近大远小的特性，平行线相交于一点。在实际的计算机图形中用得更多。

2D投影变换

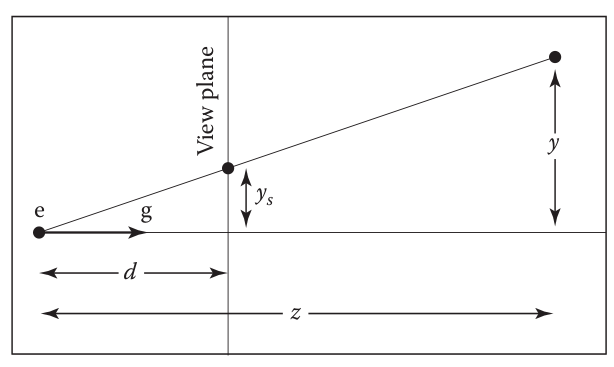
如上图所示，我们从视点$\mathbf{e}$沿着$\mathbf{g}$方向看，看到的实际的点的高度为$y$，反映在观察平面上高度为$y_s$，观察平面距离视点为$d$，实际的点距离视点为$z$，根据简单的相似三角形的关系，我们有（这里我们认为$z$是距离，为正数，而不是坐标意义下的负数）：

$$y_{s}=\frac{d}{z} y$$

虎书里还提到了线性有理变换，这里把变换矩阵简单写一下（感兴趣可以直接看虎书）

$$\left[\begin{array}{c} \tilde{x} \\ \tilde{y} \\ \tilde{z} \\ \tilde{w} \end{array}\right]=\left[\begin{array}{cccc} a_{1} & b_{1} & c_{1} & d_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} \\ a_{3} & b_{3} & c_{3} & d_{3} \\ e & f & g & h \end{array}\right]\left[\begin{array}{c} x \\ y \\ z \\ 1 \end{array}\right]$$

$$\left(x^{\prime}, y^{\prime}, z^{\prime}\right)=(\tilde{x} / \tilde{w}, \tilde{y} / \tilde{w}, \tilde{z} / \tilde{w})$$

上面的第二个公式刚好使用了[1-Transformation Matrix-变换]中注意的第二点：齐次坐标的等价性。使用上述的变换可以进行下面的操作：

前面我们已经讲了二维的情况。但是我们实际要处理的是三维的情况。经过投影变换就好像把一个棱台给变成了一个轴平行的box。这将方便我们使用正交投影变换矩阵变成CCV。

3D投影变换

这里我们就搬出之前在[Camera Transformation-相机变换]所建立的坐标系，我们依然使用$z=n$近端平面和$z=f$远端平面，并使用$z=n$近端平面作为观察平面。需要注意的是，上面的$n$和$z$在坐标系定义下都是小于$0$的。对于投影变换后的$x_s$和$y_s$，类似前面二维情况：

$$y_{s}=\frac{n}{z} y\quad x_{s}=\frac{n}{z} x$$

我们可以整理成矩阵的形式：

$$\begin{pmatrix} x\\y\\z\\1 \end{pmatrix}\Rightarrow\begin{pmatrix} nx/z\\ny/z\\\mathrm{unknown}\\1 \end{pmatrix}\triangleq\begin{pmatrix} nx\\ny\\\mathrm{unknown}\\z \end{pmatrix}$$

于是我们所要求的投影变换矩阵满足：

$$\mathbf{P}\begin{pmatrix} x\\y\\z\\1 \end{pmatrix}=\begin{pmatrix} nx\\ny\\\mathrm{unknown}\\z \end{pmatrix}\Rightarrow \mathbf{P} =\left(\begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \end{array}\right)$$

那么$z_{s}$是多少呢？对投影变换我们注意到：

1. 近端平面$z=n$的点映射以后点不发生变化。

2. 远端平面$z=f$的点映射以后z坐标不变。

根据第(1)点：近端平面$z=n$的点映射以后点不发生变化。我们有：

$$\mathbf{P}\begin{pmatrix} x\\y\\n\\1 \end{pmatrix}=\begin{pmatrix} x\\y\\n\\1 \end{pmatrix} \triangleq\begin{pmatrix} nx\\ny\\n^2\\1 \end{pmatrix}$$

所以$\mathbf{P}$的第三行形式为$\begin{pmatrix} 0\,0\,A\,B \end{pmatrix}$，前两个元素为0是因为该齐次坐标的$z$坐标为$n^2$，和$x,y$的取值无关。我们单独拿出第三行和齐次坐标相乘有：

$$\begin{pmatrix} 0 & 0 & A & B \end{pmatrix}\begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix}=n^{2}\Rightarrow An+B=n^2$$

根据第(2)点：远端平面$z=f$的点映射以后z坐标不变。我们有：

$$\left(\begin{array}{l} 0 \\ 0 \\ f \\ 1 \end{array}\right) \Rightarrow\left(\begin{array}{l} 0 \\ 0 \\ f \\ 1 \end{array}\right)\triangleq\left(\begin{array}{c} 0 \\ 0 \\ f^{2} \\ f \end{array}\right)\Rightarrow Af+B=f^2$$

于是我们有：

$$\left\{\begin{aligned} &An+B=n^2\\ &Af+B=f^2 \end{aligned}\right.\quad\Rightarrow\quad\left\{\begin{aligned} &A=n+f\\ &B=-nf \end{aligned}\right.$$

这样我们就确定了投影变换的变换矩阵：

$$\mathbf{P}=\begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -f n \\ 0 & 0 & 1 & 0 \end{bmatrix}$$

经过投影变换最终我们看到坐标发生了如下的变化：

$$\mathbf{P}\left[\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right]=\left[\begin{array}{c} n x \\ n y \\ (n+f) z-f n \\ z \end{array}\right] \triangleq\left[\begin{array}{c} \frac{n x}{z} \\ \frac{n y}{z} \\ n+f-\frac{f n}{z} \\ 1 \end{array}\right]$$

有时候我们想把屏幕坐标变换回世界坐标，这时候我们就需要用到$\mathbf{P}$的逆矩阵：

$$\mathbf{P}^{-1}=\left[\begin{array}{cccc} \frac{1}{n} & 0 & 0 & 0 \\ 0 & \frac{1}{n} & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & -\frac{1}{f n} & \frac{n+f}{f n} \end{array}\right]\triangleq\left[\begin{array}{cccc} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 0 & f n \\ 0 & 0 & -1 & n+f \end{array}\right]$$

完整的透视变换包括了正视变换和投影变换的组合，先处理近大远小的投影变换为box，然后把box变回一个CCV。

$$\mathbf{M}_{\mathrm{per}}=\mathbf{M}_{\mathrm{orth}} \mathbf{P}=\left[\begin{array}{cccc} \frac{2 n}{r-l} & 0 & \frac{l+r}{l-r} & 0 \\ 0 & \frac{2 n}{t-b} & \frac{b+t}{b-t} & 0 \\ 0 & 0 & \frac{f+n}{n-f} & \frac{2 f n}{f-n} \\ 0 & 0 & 1 & 0 \end{array}\right]$$

在OpenGL中，这一矩阵的定义可能不一样：

$$\mathbf{M}_{\text {OpenGL }}=\left[\begin{array}{cccc} \frac{2|n|}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2|n|}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & \frac{|n|+|f|}{|n|-|f|} & \frac{2|f||n|}{|n|-|f|} \\ 0 & 0 & -1 & 0 \end{array}\right]$$

这里我们使用了$\mathbf{M}_{\mathrm{orth}}$，随之而来的问题是：$\mathbf{M}_{\mathrm{orth}}$中的$l,r,t,b$这些值怎么定义呢，它们定义了我们的窗口看到的物体，由于近端平面$z=n$的$x$和$y$不变，我们这里选择了近端平面$z=n$来定义$l,r,t,b$。

我们最后来看一下从相机坐标经过透视变换到屏幕坐标的算法流程：

相机坐标经过透视变换到屏幕坐标的算法流程

2.5 Field-of-View-视场

我们通过$(l,r,t,b)$和$n$定义我们的窗口，我们可以进一步简化，如果我们屏幕的中心是原点，那么有：

$$\begin{aligned} l & =-r, \\ b & =-t . \end{aligned}$$

另外我们可以添加每个像素是正方形的约束，使得图形没有形状的畸变，我们使用的$r$和$t$一定要和水平像素数$n_x$和竖直像素数$n_y$成比例：

$$\frac{n_{x}}{n_{y}}=\frac{r}{t}$$

当$n_x$和$n_y$被确定以后，只剩下一个自由度，我们经常使用$\theta$作为视场，下图为垂直视场，它满足关系：

$$\tan\frac{\theta}{2}=\frac{t}{|n|}$$

垂直视场

通过确定$n$和$\theta$，我们就可以计算$t$来得到更一般的观测系统。

3 Graphics Pipeline-图形管线

渲染的第二种主要方法是逐个将对象绘制到屏幕上，也称为物体顺序渲染。与后面讲到的光线追踪不同，在光线追踪中我们逐个考虑每个像素并找到影响其颜色的对象，现在我们将逐个考虑每个几何对象并找到它可能影响的像素（说得有点拗口哈哈）。

找到图像中由几何图元占据的所有像素的过程称为光栅化，因此物体顺序渲染也可以称为光栅化渲染。执行从对象开始到更新图像像素结束的一系列操作被称为图形管线。

当然，物体顺序渲染不只有一种方法——两个非常不同的图形管线示例是用于通过OpenGL和Direct3D等API支持交互式渲染的硬件管线，以及用于电影制作的支持RenderMan等API的软件管线。硬件管线必须以足够快的速度运行，以实时响应游戏、可视化和用户界面。软件管线必须呈现最高质量的动画和视觉效果，并能适应庞大的场景，但可能需要更长的渲染时间。

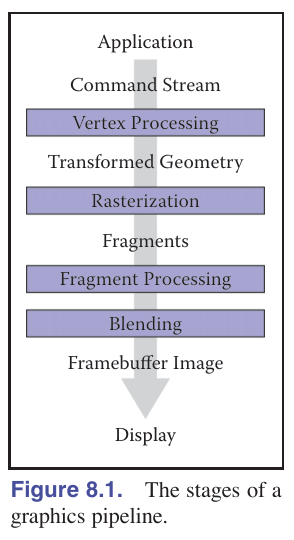
图形管线可以分为四个阶段：顶点处理、光栅化、片段处理和片段混合。

几何对象通过交互应用程序或场景描述文件输入到管线中，并且始终由一组顶点描述。顶点处理阶段对顶点进行操作，然后使用这些顶点生成基本图元发送到光栅化阶段。

物体顺序渲染的工作可以分为三个阶段：光栅化、光栅化前的几何操作和光栅化后的像素操作。几何操作中最常见的操作是应用矩阵变换，将定义几何形状的点从物体空间映射到屏幕空间，以便输入到光栅化器时以像素坐标或屏幕空间表示。像素操作中最常见的操作是隐藏面消除，使离观察者更近的表面显示在离观察者更远的表面之前。

光栅化器将每个基本图元分解为一组片段(fragment)，每个片段对应于被基本图元覆盖的像素。片段处理阶段处理各个片段，然后在片段混合阶段中将每个像素对应的片段进行合并。下面是图形管线的示意图。

3.1 光栅化